// сдвиг без умножения, перемещая символ из одного m-регистра в другой

           b[j] = b[j-1];

        // закольцовываем выходящий символ в крайний левый b0-регистр

        b[0] = alpha_to[(g[0]+feedback)%n];

     }

     else

     {  // деление завершено, осуществляем последний сдвиг регистра, на выходе регистра

        // будет частное, которое теряется, а в самом регистре – искомый остаток

        for (j = n-k-1; j>0; j--) b[j] = b[j-1] ; b[0] = 0;

     }

   }

}

Декодер (decoder)

Декодирование кодов Рида-Соломона представляет собой довольно сложную задачу, решение которой выливается в громоздкий, запутанный и чрезвычайно ненаглядный программный код, требующий от разработчика обширных знаний во многих областях высшей математики. Типовая схема декодирования, получившая название авторегрессионого спектрального метода декодирования, состоит из следующих шагов:

n  вычисления синдрома ошибки (синдромный декодер);

n  построения полинома ошибки, осуществляемое либо посредством высокоэффективного, но сложно реализуемого алгоритма Берлекэмпа-Месси, либо посредством простого, но медленного Евклидового алгоритма;

n  нахождения корней данного полинома, обычно решающееся лобовым перебором (алгоритм Ченя);

n  определения характера ошибки, сводящееся к построению битовой маски, вычисляемой на основе обращения алгоритма Форни или любого другого алгоритма обращения матрицы;

n  наконец, исправления ошибочных символов путем наложения битовой маски на информационное слово и последовательного инвертирования всех искаженных бит через операцию XOR.

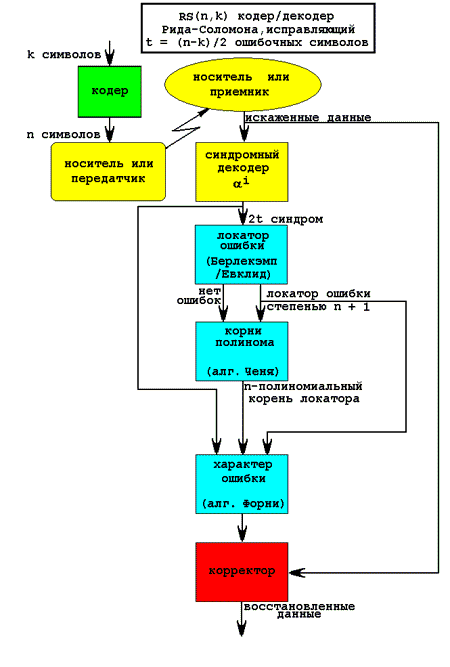
Рисунок 3. Схема авторегрессионного спектрального декодера корректирующих кодов Рида-Соломона

Синдромный декодер

Грубо говоря, синдром есть остаток деления декодируемого кодового слова c(x) на порожденный полином g(x), и, если этот остаток равен нулю, кодовое слово считается неискаженным. Ненулевой остаток свидетельствует о наличии по меньшей мере одной ошибки. Остаток от деления дает многочлен, не зависящий от исходного сообщения и определяемый исключительно характером ошибки (syndrome – греческое слово, обозначающее совокупность признаков и/или симптомов, характеризующих заболевание).

Принятое кодовое слово v с компонентами vi = c_i + e_i, где i = 0, … n – 1, представляет собой сумму кодового слова c и вектора ошибок e. Цель декодирования состоит в очистке кодового слова от вектора ошибки, описываемого полиномом синдрома и вычисляемого по формуле:  S_j = v(a^j+j0–1), где j изменяется от 1 до 2t, а a представляет собой примитивный член «альфа», который мы уже обсуждали в предыдущей статье. Да, мы снова выражаем функцию деления через умножение, поскольку деление – крайне неэффективная в смысле производительности операция.

Блок-схема устройства, осуществляющего вычисление синдрома, приведена на рис. 4. Как видно, она представляет собой типичный фильтр (сравните ее со схемой рис. 2), а потому ни в каких дополнительных пояснениях не нуждается.